
Zadanie Proste 2 (pro)
Pomóż nam usprawnić bazę zadań!
Proste 2
Limit pamięci: 64 MB
Odległością prostej od wielokąta nazywamy najmniejszą odległość jakiegokolwiek punktu należącego do tego wielokąta od tej prostej (przez wielokąt rozumiemy tu zarówno jego brzeg, jak i wnętrze). Od wielokąta nie wymagamy, żeby był wypukły, nie miał wierzchołków wielokrotnych czy samoprzecięć brzegu.
Zadanie
Napisz program który:
- wczyta ze standardowego wejścia opis wielokąta i opisy pewnej liczby prostych,
- dla każdej prostej wyznaczy najmniejszą odległość od wielokąta,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu wejścia znajdują się dwie liczby całkowite
 oraz
oraz 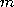 (
(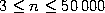 ,
, 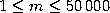 ),
oddzielone pojedynczym odstępem i oznaczające liczbę boków
wielokąta oraz liczbę prostych do przeanalizowania.
Kolejnych
),
oddzielone pojedynczym odstępem i oznaczające liczbę boków
wielokąta oraz liczbę prostych do przeanalizowania.
Kolejnych  wierszy zawiera po dwie liczby całkowite
wierszy zawiera po dwie liczby całkowite
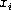 i
i 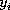 (
(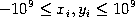 ), oddzielone pojedynczym
odstępem i oznaczające współrzędne
), oddzielone pojedynczym
odstępem i oznaczające współrzędne 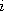 -tego wierzchołka wielokąta.
Pary wierzchołków następujące bezpośrednio po sobie, podobnie jak pierwszy i ostatni wierzchołek,
wyznaczają krawędzie wielokąta.
Następne
-tego wierzchołka wielokąta.
Pary wierzchołków następujące bezpośrednio po sobie, podobnie jak pierwszy i ostatni wierzchołek,
wyznaczają krawędzie wielokąta.
Następne 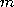 wierszy zawiera po trzy liczby całkowite
wierszy zawiera po trzy liczby całkowite
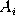 ,
, 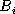 i
i 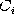 (
(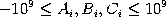 ,
, 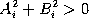 ), pooddzielane
pojedynczymi odstępami i definiujące prostą o równaniu
), pooddzielane
pojedynczymi odstępami i definiujące prostą o równaniu
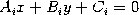 .
.
Wyjście
Wyjście powinno się składać z 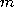 wierszy.
wierszy.
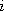 -ty wiersz wyjścia powinien zawierać kwadrat odległości
-ty wiersz wyjścia powinien zawierać kwadrat odległości
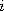 -tej prostej od wielokąta, zapisany w postaci
ułamka prostego nieskracalnego, w którym licznik od mianownika
jest oddzielony znakiem ukośnika (
-tej prostej od wielokąta, zapisany w postaci
ułamka prostego nieskracalnego, w którym licznik od mianownika
jest oddzielony znakiem ukośnika (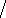 ).
).
Przykład
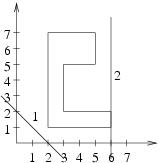
Dla danych wejściowych:
8 2 2 1 6 1 6 2 3 2 3 5 5 5 5 7 2 7 1 1 -2 1 0 -6poprawną odpowiedzią jest:
1/2 0/1
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English